ANOVA (분산분석) - 그룹간 평균을 비교하기 위한 방법
평균을 모르면 분산을 계산할 수 없습니다. 평균을 데이터셋에서 빼서 제곱을 하고 더한 후 데이터 갯수로 나눈 것이 분산이기 때문입니다.
아노바는 분산을 이용해서 평균을 추론하는 방법입니다.
ANOVA가 필요한 이유는 세 집단 이상의 평균 비교를 위해서 입니다.
연령대의 경우 20대, 30대, 40대, 50대 등과 같이 여러 개의 그룹이 생기므로 ANOVA를 사용해야 합니다.
t-test도 2개 이상의 집단에 대해 사용할 수는 있습니다.
성별과 몸무게처럼 남/녀라는 2개의 그룹이 생기는 GENDER라는 범주형 변수와 몸무게라는 1개의 연속형 변수가 있는 데이터의 경우에는 t-test를 사용할 수는 있습니다.
그러나 성별 연령대별 몸무게 평균 비교와 같은 경우에는 ANOAVA만 사용할 수 있습니다.
세 집단 이상의 평균 비교를 할 때 t-test를 사용하면 신뢰구간에 문제가 생기게 됩니다.
A-B그룹과 B-C, C-A 그룹 각각에 신뢰도 0.95를 하면 0.95의 세 제곱이 되기 때문에 작아지게 되는 것입니다.
F-분포

ANOVA의 검정통계량 F = 그룹 간 차이(변동) / 각 그룹내 차이(변동)입니다.
그룹간 차이(변동)가 각 그룹내 변동보다 뚜렷하게 클수록 검정통계량 F 값이 커지고 pr값은 작아집니다.
분산분석표
| 제곱합 | 자유도 | 평균제곱 | F값 | |
| 요인 | 그룹 간 제곱합 | K - 1 | 그룹 간 변동 | 검정통계량 = 그룹 간 변동 / 그룹 내 변동 |
| 잔차 | 그룹 내 제곱합 | N - K | 그룹 내 변동 | |
| 합계 | 전체 제곱합 | N - 1 |
** K : 처리 그룹의 수 , N : 총 관측치의 수
ANOVA에서 귀무가설은 모든 그룹의 평균이 같다, 그룹별 평균이 같다고 놓게 됩니다.
아노바에는 그룹이 여러개 있으므로, 어느 그룹인지는 모르겠지만 평균이 다른 그룹이 존재한다고 대립가설을 세우게 됩니다.
만약 대립가설을 채택하게 된다고 해도, 아노바는 어떤 그룹이 다른지는 알려주지 않습니다. 사후검정으로 수행하게 됩니다.
사후검정으로 그룹별로 되어있던 것을 짝을지어 테스트해보고 어떤 값이 달랐다는 것을 살펴보게 됩니다.
등분산 검정 - Bartlett's Test
anova를 사용하기 전에 해봐야하는 검정이 있습니다.
바틀렛 테스트는 그룹별로 분산이 같은지 확인하는 테스트입니다.
이 데이터의 그룹별 분산이 같지 않다면 아노바 말고 다른 테스트를 해야 합니다.
그룹별로 분산이 같다면 anova를 사용할 수 있습니다.

factor column에 들어있는 age_grp 별로 분산이 같은지 확인해야 합니다.
이 바틀렛 테스트에서 귀무가설은 모든 분산이 같다입니다.
검정결과 p_value가 0.05보다 큰 값이므로 귀무가설을 기각하지 못합니다.
따라서 등분산입니다. 즉 anova를 쓸 수 있는 데이터입니다.
One-way ANOVA
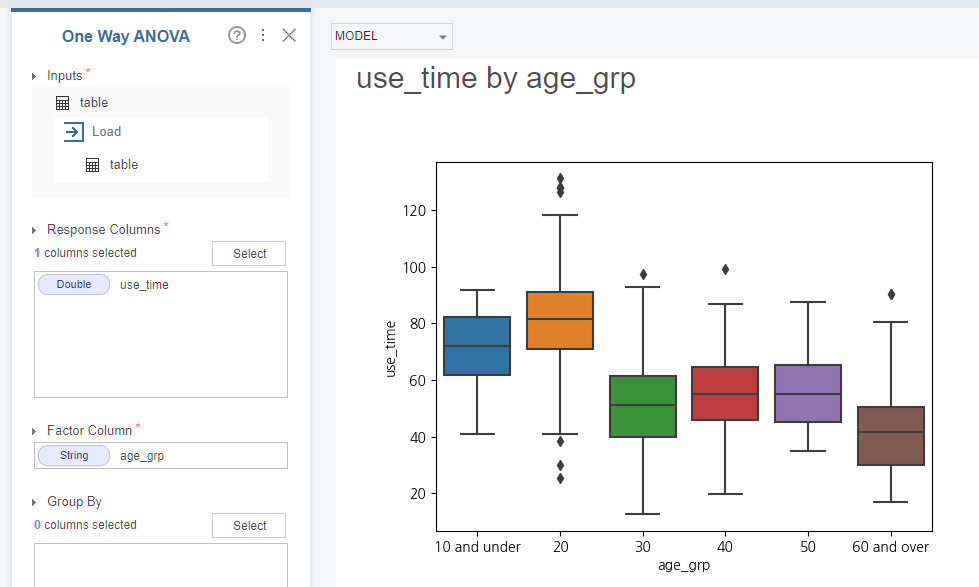


브라이틱스에서 원웨이 아노바의 함수 사용 형태는 바틀렛 테스트와 동일한 형태입니다.
검정 결과 표에서 F 값은 1505로 나왔는데 pr부분 즉 probability 확률이 0.0으로 나왔기 때문에
귀무가설을 기각하게 됩니다. 귀무가설은 평균이 같다는 것입니다. 따라서 평균이 같지 않은 그룹이 있다는 뜻입니다.
사후검정 - Tukey's range test
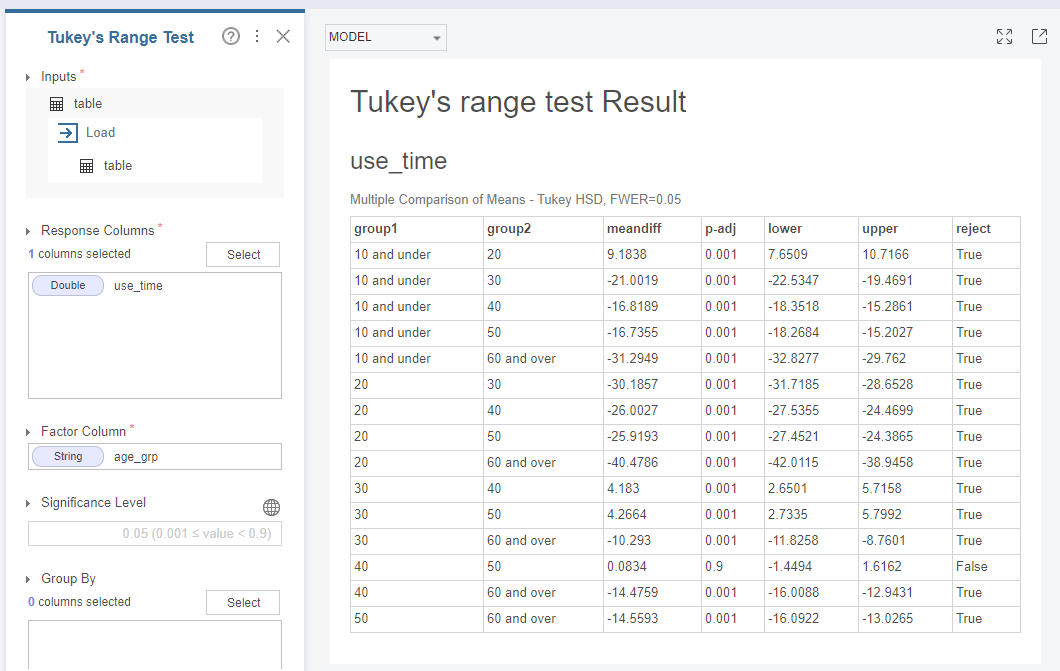
이 테스트는 10대와 20대를 비교하고, 10대와 30대를 비교하는 등, 각 그룹을 다른 그룹과 비교하는 결과를 알려줍니다.
모든 2개씩 짝지은 조합을 다 만들고 reject 컬럼에서 true 인지 false 인지를 판단하는 것입니다.
어느 조합 때문에 귀무가설이 reject 되었는지를 알려줍니다. true라는 것은 평균이 같지 않다는 뜻입니다.
false는 귀무가설 기각에 원인이 없다는 뜻입니다. 따라서 40대와 50대는 평균이 같은 데이터 였던 것입니다.

정리하면, ANOVA 는 세 단계가 있습니다.
Bartlett's Test는 ANOVA를 사용할 수 있는지를 확인하는 검정입니다. 등분산인지 검정하고, 등분산이면 ANOVA를 사용할 수 있다고 판단하면 됩니다. ANOVA는 귀무가설이 모든 집단의 평균이 같다는 것이기 때문에, 귀무가설이 기각이 되면 사후검정을 진행해서 어느 집단의 평균이 같지 않았는지 , 즉 reject 가 true인 것들이 어느 집단의 조합이었는지를 확인해주는 작업을 하게 됩니다.
'IT,SW,Data,Cloud,AI' 카테고리의 다른 글
| 빅데이터분석기사 필기 시험준비 - 나만의 암기포인트 (0) | 2021.09.30 |
|---|---|
| 머신러닝 초보자를 위한 강의와 책 추천 (0) | 2021.08.26 |
| 개발자이직 알아볼 때 점핏(jumpit) 플랫폼 사용하면 편리해요! (0) | 2021.07.27 |
| JAVA와 객체지향프로그래밍 (0) | 2021.05.31 |
| Brightics 사용법 /초보자용 꿀팁 (0) | 2021.05.19 |
| Logistic Regression, kNN(k-Nearest Neighbor), Naive Bayes (0) | 2021.04.21 |
| 상관분석이란? 상관계수 결과 해석 (0) | 2021.04.19 |
| 추론통계 기초 이해 및 Brightics를 사용한 t-test 결과 해석 (0) | 2021.04.19 |




댓글